Assignment 7 (Nov 2)¶
Today’s topics are:
Efficiency
Timing code
Using vectorized functions/methods
Easy parallelization with Numba
Readings (optional)¶
If you find this week’s material new or challenging, you may want to read through some or all the following resources while working on your assignment:
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('seaborn')
Efficiency¶
Now that we’ve learned several workflows in Python, some of which can take a long time (Monte Carlo methods and MCMC), we are going to talk about:
how to time your code
how to estimate how long your code will take (and when you can’t)
how to use vectorization to avoid slow loops
how to use Numba to speed up slow loops
Timing code¶
To understand how fast / efficient our code is, we will first need to learn how long our code takes to run.
The most basic way to time code is using the built-in Python time module.
The function time.time() gives us a timestamp from when it is called. This timstamp is a number in seconds with ~microsecond (6 decimal) precision on Linux / Mac.
Note: The precision of time on Windows is actually closer to 0.01 seconds in practice, so be careful comparing very short time periods.
import time
n = 10000000
time_start = time.time()
x = np.random.rand(n)
y = np.sort(x)
time_end = time.time()
time_delta = time_end - time_start
print(f"Time to sort {n:.0e} numbers: {time_delta:.3f} s")
Time to sort 1e+07 numbers: 1.624 s
Try re-running the above cell several times.
You should notice that the timing for each run changes slightly. This can be due to:
How much work there is to do (e.g. since randomness is involved)
How many background tasks are running on your computer when you run the cell
To get an accurate estimate of how long our code takes to run, as scientists we can run an experiment by:
Closing all background programs so only Python is running
Time our code chunk several times
Take the average and standard deviation of all of the runs
n = 10000000
timings = []
for i in range(10):
time_start = time.time()
x = np.random.rand(n)
y = np.sort(x)
time_end = time.time()
time_delta = time_end - time_start
print(f"Run {i} Time to sort {n:.0e} numbers: {time_delta:.3f} s")
timings.append(time_delta)
time_mean = np.mean(timings)
time_std = np.std(timings)
print(f"Avg time to sort {n:.0e} numbers: {time_mean:.3f} +/- {time_std:.3f} s (ntrials: {len(timings)})")
Run 0 Time to sort 1e+07 numbers: 2.335 s
Run 1 Time to sort 1e+07 numbers: 1.477 s
Run 2 Time to sort 1e+07 numbers: 1.234 s
Run 3 Time to sort 1e+07 numbers: 1.311 s
Run 4 Time to sort 1e+07 numbers: 1.330 s
Run 5 Time to sort 1e+07 numbers: 1.433 s
Run 6 Time to sort 1e+07 numbers: 1.325 s
Run 7 Time to sort 1e+07 numbers: 1.469 s
Run 8 Time to sort 1e+07 numbers: 1.681 s
Run 9 Time to sort 1e+07 numbers: 1.690 s
Avg time to sort 1e+07 numbers: 1.529 +/- 0.305 s (ntrials: 10)
Conveniently, the IPython framework that Jupyter runs on has some built-in functions for timing code. Called IPython magics, we can invoke them with % and the main ones we’ll use are time and timeit (See all IPython magics here).
%%time
x = np.random.rand(n)
y = np.sort(x)
CPU times: user 2.12 s, sys: 10.1 ms, total: 2.13 s
Wall time: 2.12 s
Here we get a dew outputs, but the one we care about is Wall time (the total time to runn the cell).
While %%time will time an entire cell If we want to time a specific line of code, we can use %time instead:
x = np.random.rand(n)
%time y = np.sort(x)
CPU times: user 1.54 s, sys: 10.2 ms, total: 1.55 s
Wall time: 1.55 s
We saw above that we often want to run our code multiple times to get the average runtime. We can do this with the %%timeit magic.
%%timeit
x = np.random.rand(n)
y = np.sort(x)
1.55 s ± 248 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
Built-in vectorized methods¶
Here we will use what we learned about timing code to investigate a few different ways of computing the maximum of a list / array. Our four options for computing the max are:
Using a for loop
Python built-in
max()NumPy function
np.max()NumPy array method
np.ndarray.max()
First let’s set up an example array to pull the maximum from:
arr = np.array([1, 7, 2, 9, 1, 2, 3, 0, 4, 8])
Now let’s show our 4 options of computing the max and make sure they work!
def max_loop(arr):
"""
Return the maximum value in an array.
"""
maxval = arr[0]
for val in arr:
if val > maxval:
maxval = val
return maxval
# 1. For loop
max1 = max_loop(arr)
print(f"For loop: {max1}")
# 2. Python max()
max2 = max(arr)
print(f"Python max(): {max2}")
# 3. NumPy np.max()
max3 = np.max(arr)
print(f"NumPy np.max(): {max3}")
# 4. NumPy array.max()
max4 = arr.max()
print(f"NumPy array.max(): {max4}")
For loop: 9
Python max(): 9
NumPy np.max(): 9
NumPy array.max(): 9
Now we have 4 ways of computing the maximum of an array, but we’ll have to test on much longer arrays to start to see differences in speed. Let’s use np.random to make a long random array.
Let’s also time our loop function with the %%timeit IPython magic (see docs).
Remember: %%magic is for a whole cell, %magic is when using inline.
%%timeit
seed = 999 # Change for different random results
rng = np.random.default_rng(seed) # Init RNG
ndraws = 1000000 # Number of random numbers to generate
# Random array of length ndraws (values between 0 and 1)
arr = rng.random(ndraws)
max1 = max_loop(arr)
88.3 ms ± 7.59 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)
Q: What is wrong with the above example?
Hint: Recall we want to time the max_loop function only.
A: What we’re actually timing above is the entire cell, including making our random array. If we want a fair comparison between our max methods, we need to isolate only the work of each function.
Let’s use the inline %timeit to time our 4 max functions.
# Compute this ahead of time so we don't time it
seed = 999 # Change for different random results
rng = np.random.default_rng(seed) # Init RNG
ndraws = 1000000 # Number of random numbers to generate
# Random array of length ndraws (values between 0 and 1)
arr = rng.random(ndraws)
# Time our 4 different methods
print('1. For loop')
max1 = %timeit max_loop(arr)
print('\n2. Python max()')
max2 = %timeit max(arr)
print('\n3. NumPy np.max()')
max3 = %timeit np.max(arr)
print('\n4. NumPy array.max()')
max4 = %timeit arr.max()
1. For loop
86.4 ms ± 6.76 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)
2. Python max()
57.9 ms ± 416 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)
3. NumPy np.max()
483 µs ± 914 ns per loop (mean ± std. dev. of 7 runs, 1000 loops each)
4. NumPy array.max()
492 µs ± 36.7 µs per loop (mean ± std. dev. of 7 runs, 1000 loops each)
Seems like we have our ranking!
np.array.max()faster thannp.max()but within errorsPython
max()for loop
We should get the same ranking if we feed in a Python list [] rather than NumPy array right?
Let’s try it:
# Compute this ahead of time so we don't time it
seed = 999 # Change for different random results
rng = np.random.default_rng(seed) # Init RNG
ndraws = 1000000 # Number of random numbers to generate
# Random array of length ndraws (values between 0 and 1)
arr = rng.random(ndraws)
lst = list(arr)
# Time our 4 different methods
print('1. For loop')
max1 = %timeit max_loop(lst)
print('\n2. Python max()')
max2 = %timeit max(lst)
print('\n3. NumPy np.max()')
max3 = %timeit np.max(lst)
print('\n4. NumPy array.max()')
max4 = %timeit np.array(lst).max()
1. For loop
39.5 ms ± 792 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)
2. Python max()
23.7 ms ± 178 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)
3. NumPy np.max()
42.1 ms ± 98.7 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)
4. NumPy array.max()
42.1 ms ± 455 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)
What happened here? It seems like the ranking switched:
Python
max()np.max()faster thannp.array.max()but within errorsfor loop
This brings up an interesting subtlety about coding in Python (and in general):
The data structure you choose can affect the efficiency of your program
Why is this happening? To find out, we’ll notice 2 things about our timings.
The
np.maxandnp.array.max()methods were faster on NumPy arraysThe built-in Python
maxmethod was faster on the Python list[]
We could chalk this up to a platitude like,
“Python max() is optimized for Python lists, while np.max() is optimized for NumPy arrays”.
While this is partially true, if we understand the differences between lists and arrays, we can see there’s a bit more going on here.
Python list |
NumPy array |
|---|---|
Can contain any object |
Contains numerical data |
No fixed type (size) of elements |
Fixed data type (size) of elements |
No |
Has |
Let’s verify the data type of our NumPy array:
arr.dtype
dtype('float64')
The fact that a NumPy array has a fixed data type and a defined length means that functions like np.max() can take advantage of super fast low-level algorithms (which run as compiled C code) to search, do math, comparisons, etc on our array.
When a NumPy array is created, it blocks out a certain chunk of your computer’s memory so that all future operations on the array are speedy! BUT this takes a bit of time to save time later.
To find a maximum, all of our methods need to look at every element in the list/array, BUT NumPy is faster for 2 reasons:
it blocks off a place in memory
the max function can very quickly in C
So why aren’t the NumPy functions faster on lists as well?
As you can see in the line %timeit np.array(lst).max(), the Python list had no .max() so we had to first convert the data type from list to NumPy array and then call .max(). This is also what is happening below the hood when we call np.max(lst) on a regular list.
So the reason Python max() is slower on arrays is that NumPy has to block off memory and then convert the list to an array (which takes time), before running the speedier NumPy algorithm on it. Overall, converting to an array and then finding the max is slower than just finding the max (like Python does with max()).
This leads us to our rules of thumb for efficient science code:
Efficiency pro tips¶
Use the proper data structure for the job
NumPy arrays are suited for numerical data
Pandas DataFrames are suited for table data
Python Lists are suited to non-numerical or mixed type data
Use the optimized built-in functions
Use NumPy’s functions/methods on arrays
Use the Pandas methods on DataFrames
Avoid converting back and forth between data types
Keep your numerical data in NumPy arrays wherever possible
Keep your table data in DataFrames wherever possible
If you need to compute values in a loop, initialize your arrays (e.g with
np.zeros) before the loop
Avoid custom Python loops wherever possible (see rule 2)
Time scaling¶
The scaling behavior of our code describes how quickly it runs as the inputs get larger. Let’s use our max situation again.
There were 8 situations total:
np.max(array) and np.max(list)
array.max() and np.array(list).max()
max(array) and max(list)
max_loop(array) and max_loop(list)
Let’s look at the best from each category we identified before, so:
np.max(array)
array.max()
max(list)
max_loop(list)
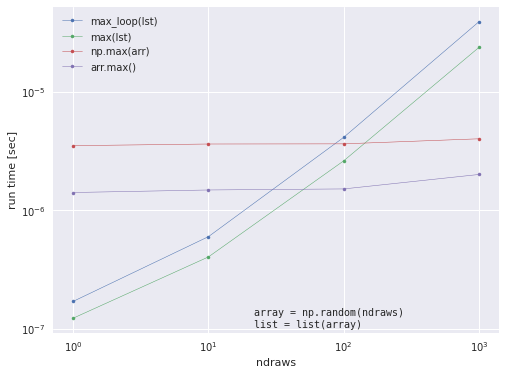
To investigate the scaling behavior, we will run the timing code with increasing ndraws (length of random array).
Note: Most operations (like max) will take exponentially longer as the array size increases. For now, we will only show ndraws = [10, 100, 1000], but will use parallel programming (multiprocessing) later to speed things up!
%time
seed = 999 # Change for different random results
rng = np.random.default_rng(seed) # Init RNG
ndraws_list = [1, 10, 100, 1000] # Number of random numbers to generate
timings = np.zeros((len(ndraws_list), 4))
for i, ndraws in enumerate(ndraws_list):
arr = rng.random(ndraws)
lst = list(arr)
t1 = %timeit -o -q max_loop(lst)
timings[i, 0] = t1.average
t2 = %timeit -o -q max(lst)
timings[i, 1] = t2.average
t3 = %timeit -o -q np.max(arr)
timings[i, 2] = t3.average
t4 = %timeit -o -q arr.max()
timings[i, 3] = t4.average
CPU times: user 2 µs, sys: 0 ns, total: 2 µs
Wall time: 5.01 µs
label_names = ['max_loop(lst)', 'max(lst)', 'np.max(arr)', 'arr.max()']
# plot the data
f = plt.figure(facecolor='white', figsize=(8, 6))
ax = plt.subplot(111)
for i, label in enumerate(label_names):
ax.plot(ndraws_list, timings[:, i], '.-', lw=.5, label=label)
ax.set_xlabel('ndraws', fontname='Helvetica')
ax.set_ylabel(r'run time [sec]', fontname='Helvetica')
ax.set_xscale('log')
ax.set_yscale('log')
ax.legend()
ax.text(0.45, 0.01, "array = np.random(ndraws)\nlist = list(array)", ha='left',
va='bottom', transform=ax.transAxes, family='monospace')
plt.show()
findfont: Font family ['Helvetica'] not found. Falling back to DejaVu Sans.
Parallel computing (multiprocessing)¶
Every compute these days has several CPUs or “cores” which can each run several “threads” to do work / run code / render cat pictures at a time. By default, Python is single-threaded and can only use one thread / process at a time.
Using the built-in multiprocessing library, or some packages that we’ll introduce here, we will see how to run our code in parallel using multiple threads or processes at a time. This a deep topic, so we will only have time to introduce the concepts and will point you towards deeper tutorials with more info on parallel computing as we go along.
Reading:
PQDM¶
One way of parallelizing our code is using the pqdm module (see docs at Parallel TQDM (pqdm)), an extension of the tqdm module which lets us time our code with a cool progress bar.
To get pqdm, activate your conda environment and run:
conda install -c conda-forge pqdm
It will come with the package, tqdm which means “progress” in Arabic (see docs here).
The main function of tqdm is to have a progress bar for your loops. Just wrap your loop iterable e.g. tqdm(range(10)) and you’ll see a progress bar with the average time to run each iteration and estimated total run time.
from tqdm import tqdm
import time
for i in tqdm(range(10)):
# Choose random sleep time between 0 and 3 seconds
time.sleep(np.random.randint(0, 3))
100%|██████████| 10/10 [00:11<00:00, 1.10s/it]
This is cool, but we really care about the parallel functionality provided by pqdm. To use it, we need to choose between threads and processes (if you don’t know the difference, stick to processes for now!).
threads:
from pqdm.threads import pqdmprocesses:
from pqdm.processes import pqdm
The program we will parallelize is a function that computes the nth Fibonacci number.
The Fibonacci sequence is defined as the sequence starting at 1, where each term is added to the previous one. E.g.
1, 1, 2, 3, 5, 8, 13, ...
To compute the nth Fibonacci number, we can use the following recursive function. A recursive function is one that calls itself. See more about recursion in this Real Python video.
The important thing to note is that to compute the nth Fibonacci number, we also need the (n-1), (n-2), (n-3)… terms until we get to 1. The time to compute all these numbers gets exponentially longer at bigger n.
from pqdm.processes import pqdm
# from pqdm.threads import pqdm
def fibonacci(n):
"""
Return the nth Fibonacci number recursively.
"""
if n <= 1:
return n
else:
return(fibonacci(n-1) + fibonacci(n-2))
# Test the program works
for i in range(10):
print(fibonacci(i), end=',')
print('...')
0,1,1,2,3,5,8,13,21,34,...
Let’s time how long our code takes with larger n. This is overkill, but we’ll use both the %%time and the tqdm progress bar.
%%time
result = []
for i in tqdm(range(36)):
result.append(fibonacci(i))
print(result)
100%|██████████| 36/36 [00:06<00:00, 5.38it/s]
[0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, 514229, 832040, 1346269, 2178309, 3524578, 5702887, 9227465]
CPU times: user 6.71 s, sys: 0 ns, total: 6.71 s
Wall time: 6.7 s
Now let’s break up our loop and let pqdm do it’s magic. To run pqdm, we need the list of inputs to the function (in the above loop, it’s just range(36)), the name of the function (fibonacci), and the number of jobs we want to split the work into (usually the number of cores on your computer is a good choice. I’m on a quad core PC, so i’ll use n_jobs=4).
%%time
# To use pqdm, we need the list of values (range(36)), the function
result = pqdm(range(36), fibonacci, n_jobs=4)
print(result)
[0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, 514229, 832040, 1346269, 2178309, 3524578, 5702887, 9227465]
CPU times: user 153 ms, sys: 50.3 ms, total: 204 ms
Wall time: 3.78 s
Woohoo we cut down the runtime! Try with larger n to see how much faster we can get it with the power of parallel computing.
We can also use pqdm to run through our previous example timing the max functions. We should be able to test longer arrays now that we can compute in parallel… Let’s try it on ndraws_list = [10, 100, 1000, 10000, 100000, 1000000]. All we need to do is wrap our previous code in a function and we’ll be good to go!
rng = np.random.default_rng(999)
ndraws_list = [10, 100, 1000, 10000, 100000, 1000000]
def run_timeit(ndraws):
arr = rng.random(ndraws)
lst = list(arr)
timings = np.zeros(4)
t1 = %timeit -r 4 -o -q max_loop(lst)
timings[0] = t1.average
t2 = %timeit -r 4 -o -q max(lst)
timings[1] = t2.average
t3 = %timeit -r 4 -o -q np.max(arr)
timings[2] = t3.average
t4 = %timeit -r 4 -o -q arr.max()
timings[3] = t4.average
return timings
# This time we'll use the same number of jobs as the length of our list
out = pqdm(ndraws_list, run_timeit, n_jobs=len(ndraws_list))
# In a Linux/Mac terminal, use `top` or `htop` to see processes and CPU usage
# transfer list to array
timings = np.array(out)
label_names = ['max_loop(lst)', 'max(lst)', 'np.max(arr)', 'arr.max()']
# plot the data
f = plt.figure(facecolor='white', figsize=(8, 6))
ax = plt.subplot(111)
for i, label in enumerate(label_names):
ax.plot(ndraws_list, timings[:, i], '.-', lw=.5, label=label)
ax.set_xlabel('ndraws', fontname='Helvetica')
ax.set_ylabel(r'run time [sec]', fontname='Helvetica')
ax.set_xscale('log')
ax.set_yscale('log')
ax.legend()
ax.text(0.45, 0.01, "array = np.random(ndraws)\nlist = list(array)", ha='left',
va='bottom', transform=ax.transAxes, family='monospace')
plt.show()
plt.show()
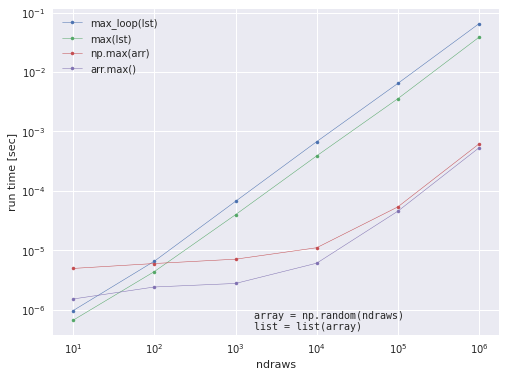
Here, we see that our previous scaling test of the max function up to \(10^4\) was misleading because the slope changes a lot for \(n=10^5\) and \(n=10^6\). This is why it’s important to test timings for “large enough” n, and simple parallelization with pqdm can help us do it quickly!
Numba¶
Here, we will give a quick example of how to use a package called numba to automatically compile your Python code to C which can magically speed up your code.
You can install Numba with:
conda install -c conda-forge numba
We highly recommend checking out this more detailed Introduction to Numba by New York University. It has step by step tutorial like this textbook and practice problems as well.
Other Numba resources:
The example we will use is the Monte Carlo calculation of pi we did before!
Let’s time our original solutions first (for loop and vectorized).
# Use this number of draws for our MC examples
n_draws = int(1e8)
Method 1: Python code only (for loop, no NumPy, no Numba)¶
To solve our problem with only Python, we will have to use the built-in random module in Python.
import random
def python_pi(n):
n_in_circle = 0
for _ in range(n):
x = random.random()
y = random.random()
if (x**2 + y**2 < 1):
n_in_circle += 1
return 4*n_in_circle / n
%timeit -r 4 python_pi(n_draws)
40.5 s ± 1.28 s per loop (mean ± std. dev. of 4 runs, 1 loop each)
Method 2: Use NumPy random (for loop, NumPy, no Numba)¶
Here we will use the NumPy basic random functions np.random.random(). Normally we want to use a RNG object, but we’ll skip it for the sake for this example.
import numpy as np
def numpy_pi(n):
n_in_circle = 0
for _ in range(n):
x = np.random.random()
y = np.random.random()
if (x**2+y**2 < 1):
n_in_circle += 1
return 4*n_in_circle / n
%timeit -r 4 numpy_pi(n_draws)
2min 11s ± 13.2 s per loop (mean ± std. dev. of 4 runs, 1 loop each)
Method 3: Use NumPy arrays (vectors, NumPy, no Numba)¶
Here, we will skip the for loop entirely. We make our x and y random arrays and feed them into our equation of a circle directly. This is the vectorized solution.
def numpy_vector_pi(n):
x = np.random.random(n)
y = np.random.random(n)
n_in_circle = len(np.where(x**2+y**2 < 1)[0])
return 4*n_in_circle / n
%timeit -r 4 numpy_vector_pi(n_draws)
5.58 s ± 916 ms per loop (mean ± std. dev. of 4 runs, 1 loop each)
We can gain a little speed by avoiding creating intermediate arrays x and y, as well as using the simple sum of the True values in our equation rather than np.where.
def numpy_vector_pi(n):
n_in_circle = np.sum(np.random.random(n)**2 + np.random.random(n)**2 < 1)
return 4*n_in_circle / n
%timeit -r 4 numpy_vector_pi(n_draws)
3.52 s ± 646 ms per loop (mean ± std. dev. of 4 runs, 1 loop each)
This vectorized solution is about as quick as we can get just with Python / NumPy.
Method 4: Use Numba to speed up Python loop (for loop, no NumPy, Numba)¶
Numba has 2 main decorators that we can use to magically translate our function to compiled C code:
jit: basicnjit: “no python” mode, skips Python things
Note: A decorator is a special type of function that changes the behavior of another function. We use a decorator with the @ symbol on the line before a function definition, e.g.:
@decorator
def func():
# do stuff
The njit is a short form for jit(nopython=True). This is usually the one we want (Numba will automatically change njit to jit if it needs to).
from numba import njit
@njit
def numba_pi(n):
n_in_circle = 0
for _ in range(n):
x = random.random()
y = random.random()
if (x**2+y**2 < 1):
n_in_circle += 1
return 4*n_in_circle / n
%timeit -r 4 numba_pi(n_draws)
1.65 s ± 77.6 ms per loop (mean ± std. dev. of 4 runs, 1 loop each)
Method 5: Use Numba with NumPy loop (for loop, NumPy, Numba)¶
Here we’ll try using Numba on the Method 2 example.
@njit
def numba_numpy_pi(n):
n_in_circle = 0
for _ in range(n):
x = np.random.random()
y = np.random.random()
if (x**2+y**2 < 1):
n_in_circle += 1
return 4*n_in_circle / n
%timeit -r 4 numba_numpy_pi(n_draws)
1.54 s ± 47 ms per loop (mean ± std. dev. of 4 runs, 1 loop each)
Method 7: Use Numba with vectorized code (vector, NumPy, Numba)¶
Here we will use Numba on Method 3.
@njit
def numba_numpy_vector_pi(n):
n_in_circle = np.sum(np.random.random(n)**2 + np.random.random(n)**2 < 1)
return 4*n_in_circle / n
%timeit -r 4 numba_numpy_vector_pi(n_draws)
3.75 s ± 843 ms per loop (mean ± std. dev. of 4 runs, 1 loop each)
Method 8: Use Numba in parallel (for loop, NumPy, Numba parallel)¶
We can add the option (parallel=True) to our Numba decorators to have it parallelize our loop automatically.
One thing we have to do here is define our output array ahead of time so Numba knows where to store the parallel results.
@njit(parallel=True)
def numba_parallel_pi(n):
n_in_circle = np.zeros(n)
for i in range(n):
x = np.random.random()
y = np.random.random()
if (x**2+y**2 < 1):
n_in_circle[i] = 1
return 4*np.sum(n_in_circle) / n
%timeit -r 4 numba_parallel_pi(n_draws)
2.07 s ± 177 ms per loop (mean ± std. dev. of 4 runs, 1 loop each)
So it seems parallelization doesn’t always speed up our work. The main reason is overhead.
Overhead is the extra time introduced by our clever speedup techniques. Some of the hidden overhead in the above examples were:
Creating a large NumPy array
Having Numba convert our code to C
Having Numba parallelize our code (send it to different processes and wait for a result)
If the work we are doing is really easy, the overhead we introduce by running it through Numba or parallelizing it can take just as long or longer than the work itself!
This is why it is important to be able to run quick timing tests with small parts of our code before we dedicate a lot of time to making it more efficient!
[Assignment 1] Improving code efficiency¶
In this assignment, you will be given a function that computes the factorial of a number using a for loop.
You will need to develop the following alternatives to the given function:
a. Same function using the Numba
@njitdecoratorb. Same function using parallel Numba
@njit(parallel=True)c. An alternative function for computing factorials (try googling for a NumPy function that might help)
Once you have your functions:
Time each for a range of n values
Plot the scaling behavior (time vs. n)
Conclude which function performs the best at high n
def factorial(n):
if n == 1:
return 1
else:
return n * factorial(n-1)
# [your code here]
[Assignment 2]¶
For this assignment you may need to do some reading / research to learn how to use a new decorator. Often in scientific programming we become aware of a tool but don’t know exactly how to use it.
The name of the decorator you need to use is lru_cache. Using google, your peers, and/or the “#help” channel in Slack, apply @lru_cache to the fibonacci(n) function we used before.
Time the function for a range of n values before and after using lru_cache and plot the scaling behavior like above.
Write a brief description of what lru_cache does and include a link to the official documentation.
Note: Make sure the highest n value you use takes at least 1 minute to compute the function (without lru_cache) below.
def fibonacci(n):
"""
Return the nth Fibonacci number recursively.
"""
if n <= 1:
return n
else:
return(fibonacci(n-1) + fibonacci(n-2))
# [your code here]
