Assignment 1 (Sep 21)¶
Welcome to assignment 1! In class we will cover the following topics:
Note
Lecture recording links will be uploaded after each class to the syllabus here.
Quick Jupyter interface tour
Difference between a
listand anumpy.arrayin pythonHow to make a function
Simple plotting with
matplotlib.pyplot
Readings (optional)¶
If you find this week’s material new or challenging, you may want to read through some or all the following SPIRL chapters before turning in your assignment:
VS Code Setup¶
Extensions: This week we will use the following Extensions. In Visual Studio Code, head to the Extensions icon in the left sidebar (icon with 4 squares) and search for / install:
PythonGitHub Pull Requests and IssuesGitLens -- Git supercharged
They should appear under the heading Installed when they are ready.
Log in with GitHub: Also click the Accounts icon in the left sidebar and are logged into your GitHub account. It should show: username (GitHub) when you are signed in.
You may need to reload the window after installing / signing in.
Note
You may reload VS Code at any time by pressing ⌃ Control ⇧ Shift P (Mac: ⌘ Command ⇧ Shift P), typing Reload Window and then pressing Enter.
Free Fall¶
We can compute math equations in Python just like we would using a calculator. We’ll first define the variables g and t and then type the equation. We write the variables first because python executes code line by line. If we put the equation first, python would get mad because it wouldn’t know what g and t were in the equation. So here’s how we do this…
For more info please see 3.3. Basic Data Types.
g_earth = 9.80665 # m/s
fall_time = 10 # sec
H = (1/2) * g_earth * fall_time**2
# print(H)
print('We will fall about {:1.2f} m on Earth after {:} sec'.format(H, fall_time))
Python list vs. Numpy array¶
What if we want to compute the falling height at several times?
fall_time = [1, 2, 3, 4, 5, 6] # [seconds]
H = (1/2) * g_earth * fall_time**2
print(H)
Here we get an error because the python list does not allow us to do math on it directly. We will use a NumPy array instead!
What is NumPy?¶
NumPy is a fundamental package for scientific computing in Python. It provides a mathematical array/matrix object that we can perform computations on! It also allows us to quickly select data or perform operations on arrays, including:
math (add/subtract, multiply/divide, dot/cross products, etc.)
logical (union, intersection, complement, etc.)
shape manipulation
sorting
reading/writing to files (I/O)
Fourier transforms
basic stats and curve fitting
random simulations
and much more…
Vectorization makes NumPy Fast!¶
When working with NumPy arrays, most operations are optimized in pre-compiled C code. That means that without ever needing to learn the C programming language, you can use code that runs as fast and efficiently as C right from Python. Writing code that uses arrays rather than looping through each element is called Vectorization and can make your programs many times faster!
Stay tuned for later weeks when we will practice converting loops into arrays.
Read more on NumPy official site: https://numpy.org/doc/stable/
Read about the basics of NumPy on SPIRL: Ch. 4.2 Numpy
Using NumPy¶
To use NumPy, we need to import the numpy library which is usually done like so:
import numpy as np
We can convert a python list containing numbers (int and/or float) to a numpy array like so:
python_list = [1, 2, 3, 4, 5, 6]
# Converting a python list into a NumPy array
numpy_array = np.array(python_list)
We can check the type of an object in Python with the type() function:
print('Python type:', type(python_list))
print('NumPy type:', type(numpy_array))
List/Array/String Indexing¶
We can index a NumPy array similarly to a Python str or list either from the front (starting at 0) or from the end (starting at -1).
See more on SPIRL 3.3.7. Str indexing
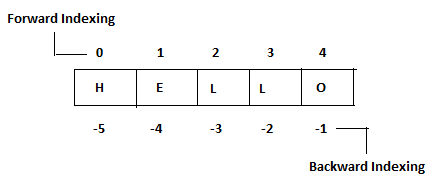
For an array, our values are numbers instead of characters so if our array is
array = np.array([11, 22, 33, 44, 55])
We could access each element like:
Forward indexing |
0 |
1 |
2 |
3 |
4 |
Array |
11 |
22 |
33 |
44 |
55 |
Backward indexing |
-5 |
-4 |
-3 |
-2 |
-1 |
test_list = [11, 22, 33, 44, 55]
test_array = np.array(test_list)
print(test_list)
print(test_array)
print(test_list[0])
print(test_array[0])
## What if you only want [22,33,44] ??
Array generation with NumPy¶
There are many built-in NumPy functions that make it easy to make new arrays. For example:
np.zeros(): Make an array of all 0snp.ones(): Make an array of all 1snp.arange(): Make an array that ranges between two values increasing by a certain step sizenp.linspace(): Make an array that ranges between two values and is a fixed lengthnp.logspace(): Make an array that ranges between two powers of 10, is a fixed length, and takes logarithmic step sizesand more…
Try it yourself, call help(np.funcname), or google for more info!
(Demo do a search on np.arange)
g_earth = 9.80665 # m/s
fall_time = np.arange(0, 100, 5) # sec
H = (1/2) * g_earth * fall_time**2
print(H)
H_delta = H[-1] - H[0]
print(f'After {fall_time.max():1.0f} sec, we will fall {H_delta:1.2f} m on Earth' )
How to make a function¶
Another way of computing this equation is by defining a Function. All functions are set up like f(x), where f is the function name and x is the parameter that goes into the function.
To define a function, we use the def command in Python. This line defines the function name and parameter(s). Any code in the body of the function must be indented and will only be run when the function is called. We will do our calculation in the function body and output the final result using the return command.
See Ch. 3.5 Functions for more info.
Let’s define a function below:
# !! Indentation is very important in python !!
def free_fall_h(t):
g = 9.80665 # m/s
H = 0.5 * g * t**2
return H
A final critical part of Python functions are the docstrings. A docstring tells future users of your code (including future you!) what your function does, what parameter(s) it takes and what it returns. Docstrings are denoted with triple quotes """.
def free_fall_h(t):
"""Return free fall distance given time t on Earth.
Args:
t (float or np.array): Time in [s]
Returns:
[float or np.array]: Free fall distance in [m]
"""
g = 9.80665 # m/s
H = 0.5 * g * t**2
return H
# fall_time = np.arange(0, 100, 5)
height = free_fall_h(fall_time)
height_delta = height[-1] - height[0]
print(f'After {fall_time.max():1.0f} sec, we will fall {height_delta:1.2f} m on Earth' )
[hands-on] A Function with 2 Parameters¶
Now that we’ve made a function with one parameter (t or time), let’s try modifying free_fall_h to make it more general so we can calculate the fallen height on different planets with different g values. Hint: you’ll now be creating an f(x,y) function with the following equation.
def free_fall_h_grav():
return
Now try using different values of g for different planets (provided below) to test if your free fall height gets larger or smaller with g:
Planet |
g (\(m/s^2\)) |
|---|---|
Mercury |
3.61 |
Venus |
8.83 |
Mars |
3.75 |
Jupiter |
26.0 |
Saturn |
11.2 |
Uranus |
10.5 |
Neptune |
13.3 |
Pluto |
0.61 |
g = 9.80665 # m/s <--- change me
height = free_fall_h_grav(fall_time, g)
print(f'After {height.max():1.0f} sec, we will fall {height_delta:1.2f} m')
Saving our work with git commit¶
Open
Source Controlside panelClick the
+sign beside the file name to stage the changesType in commit message, and then click
check boxabove tocommit
Great! Now you have a commit (Git checkpoint) on your local computer.
Free Fall – plotting with matplotlib.pyplot¶
We’re now going to plot free fall times from the functions we’ve created above using matplotlib, which we import like so:
import matplotlib.pyplot as plt
x = np.arange(0, 100, 5)
y = free_fall_h(x)
plt.figure(facecolor='white', dpi=100)
plt.plot(x, y, '.-', ms=3, c='tab:blue')
plt.text(10, 30000, 'H(t)=$\\frac{1}{2}gt^2$', size=20)
plt.title('Free fall curve on Earth')
plt.ylabel('Distance [km]')
plt.xlabel('Time [sec]')
plt.show()
[Assignment] Plot Planck function¶
Using what we learned today and the equation shown in the plot below, define the the Planck function and use it to plot the blackbody curves. Plot 4 blackbody curves with T = 6000, 5000, 4000, and 3000 K, and make sure you have the same axes scale and range as it shows in the figure below.
Be careful of the units on both axes.
Note that \(\lambda\) is short for wavelength, \(T\) is short for temperature and that you may need to google the following constants for your function (pay attention to units!):
Symbol |
Meaning |
|---|---|
\(\pi\) |
Pi |
\(c\) |
Speed of light |
\(h\) |
Planck’s constant |
\(k\) |
Boltzmann constant |
(Optional): For an extra challenge, try to replicate the color and formatting of the plot shown below. You can find lots of matplotlib customization and plotting examples here.

def planck(wavelength):
"""Return blackbody power density using the Planck function.
Parameters
----------
wavelength (array): Wavelength in [nm]
Return
------
radiance (array): Power density in [W/m^3]
"""
# your code here
return
# Define your wavelength array and call planck function here
# Make your plot here
(Optional) For more practice or to learn some handy Astropy tips, check out the Assignment 1 (BONUS) on the next page.
When you are done with your assignment, make sure to:
Stage your changes with
+Commit your changes with a descriptive message with
checkmarkPush your changes to your fork with
... menu -> push[Do it once only] Open a Pull Request on the source control tab (make sure to choose the remote branch with your username from the dropdown!)
Review the submission guide here or reach out on the #help channel on Slack if you have any questions!
